课程题目:An introduction to Poisson geometry : a minicourse
授 课 人:Camilo Andres Angulo Santacruz 博士后
所在单位:巴西弗鲁米嫩塞联邦大学
课程地点:ZOOM ID:862 062 0549,密码:2022
Zoom会议链接:https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
校内联系人:生云鹤 shengyh@jlu.edu.cn
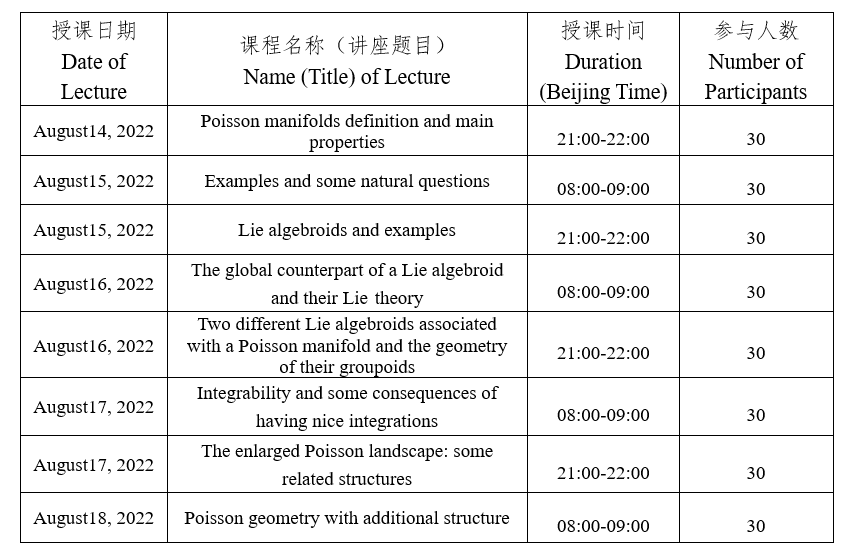
课程介绍:Poisson geometry is a lively area of research that lies at the crossroads of several fields in mathematics. On the one hand, it lies at the intersection of symplectic geometry, Lie theory, and foliation theory; and on the other, it serves as the background for several theories in mathematical physics. Though Poisson brackets can be traced back to the XIXth century, its current incarnation started in the late 1970s with the work of Lichnerowicz and rapidly developed as a field in its own right as well as through connections with other areas of mathematics. In this mini-course, we aim at introducing Poisson manifolds and offer a panoramic view of some classical and modern developments of the theory. We will start with basic definitions and properties of Poisson manifolds, some foundational results, and a wealth of examples. We will then discuss the connection to Lie theory exploring the larger world of Lie algebroids and Lie groupoids and their geometry. We will recognize that the algebroids naturally associated with Poisson manifolds come with additional geometric structures and discuss when these can be integrated to multiplicative structures on their Lie groupoids. Lastly, we will gloss over a collection of related structures and close with a particular class of examples: Poisson-Lie groups.
报告人简介:Camilo Andres Angulo Santacruz,巴西弗鲁米嫩塞联邦大学博士后,从事泊松几何,高阶李理论的Van Est定理研究。 在Commun. Contemp. Math.,J. Math. Phys.等杂志上发表多篇高水平论文。